Light

computational design

The convergence of computation and materialization enables individual multifacetted designs. Using state-of-the-art mathematical research thereby allows to virtually rebuild natural processes on any level of detail. These models are often associated with spontaneous symmetry breaking and pattern formation, and lead to new aesthetic possibilities in design, which become realizable using additive manufacturing technology. This general concept is realized for the design of a lamp using the process of spinodal decomposition in a binary alloy. The outer form, a simple cube with rounded edges and corners, thereby describes the equilibrium form the system evolves to, if time goes to infinity. The inner form, the interface between the decomposed components of the alloy after a finite time, provide the individual structure responsible for light refraction and transmission.

physics background

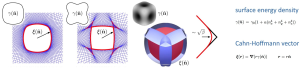
Spinodal decomposition is a mechanism for the rapid unmixing of a binary alloy from one thermodynamic phase, to form two coexisting phases. The interface between the phases is associated with a surface tension, which drives the system to coarsen and thus to reduce the interface. The resulting structure of the process determines the materials properties and can be observed on a microscopic length scale. For crystalline materials the surface tension favors certain orientations, which leads for the described functional form to facets along the orientations [100], [010] and [001].

The equilibrium configuration, the system evolves to, can be described by the Wulff construction. Considering a polar plot of the surface tension as a function of orientation allows to graphically determine the crystal faces by drawing lines from the origin to every point on the polar plot. The inner envelop of the planes perpendicular to the normal at each intersection point with the polar plot forms the equilibrium shape of the crystal.

mathematical description

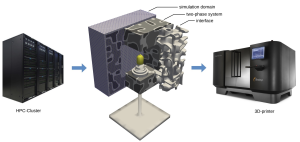
The coarsening process can be described mathematically. The idea is to define an order parameter as a function of space and time, which is 1 in one phase, 0 in the other phase and which smoothly varies between 0 and 1 over a small length scale. The Cahn-Hilliard equation defines a conserved evolution equation for this order parameter and models the coarsening process. It is a nonlinear higher order partial differential equation and can be solved numerically by discretizing the domain using a computational grid and computing the order parameter at each grid point. An adaptive finite element method is used for this purpose and the resulting system is solved on a high performance computer in each time step.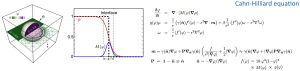

technical issues

The surface between the two phases can be extracted from the computed solution. It is implicitly described as the 0.5 level set of the order parameter. Through various postprocessing steps this surface is transformed in an appropriate format and 3D printed together with the bulb socket and the support for the stand. The used material is polyamide. The cube is 13 x 13 x 13 cm.

individualization

The realization of the design depends on the initial condition provided for the computation, which is chosen randomly with the only requirement of an equal distribution of the two phases. All realizations look similar and provide the same pleasantly diffuse impression of light. Besides the additional effort for computation and postprocessing, due to the used 3D printing technology, this individualization of the lamp comes with no additional cost.

The lamp received a honorable mention at the VMODERN furnature design competition 2015.